Koordinatensystem: Unterschied zwischen den Versionen
(Umstellungen, kleine Ergänzungen) |
K (→Sphärische Koordinatensysteme: Streichung der Flächengleichung - hat in der Geodäsie keine Bedeutung) |
||
| (2 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| − | Zur Festlegung eines Punktes auf der Erde werden '''Koordinatensysteme''' verwendet, die geeignet sind, den dreidimensionalen Raum abzubilden. Üblicherweise benutzt man sphärische oder | + | Zur Festlegung eines Punktes auf der Erde werden '''Koordinatensysteme''' verwendet, die geeignet sind, den dreidimensionalen Raum abzubilden. Üblicherweise benutzt man rechtwinklige sphärische oder ebene Lagekoordinaten auf einer Bezugsfläche, die eine Annäherung der Erdoberfläche bildet, ergänzt um eine Höhenangabe, meist auf einer anderen Bezugsfläche, die angenähert die Meeresoberfläche ist. Die Raumfahrt, die EDV und insbesondere das [[Global Positioning System]] (GPS) haben dazu geführt, dass Koordinatenberechnungen nunmehr auch in rechtwinkligen X, Y, Z-Koordinatensystemen ausgeführt werden. |
| + | |||
| + | Die Lagebezugsflächen werden werden auch als [[Geodätisches Datum|Geodätisches Datum oder Geodätisches Bezugssystem]] bezeichnet. In moderne Bezugssyteme ([[WGS84]] usw.) wird auch die Höhenbezugsfläche mit einbezogen. | ||
== Geographische Koordinaten == | == Geographische Koordinaten == | ||
| Zeile 6: | Zeile 8: | ||
Um die geografische Lage eines Ortes auf der [[Erde]] anzugeben, können verschiedene [[:de:Koordinatensystem|Koordinatensystem]]e werden verwendet. Die geographischen Koordinaten sind aber die am häufigsten verwendete Möglichkeit, die Lage auf der Erdoberfläche zu beschreiben. | Um die geografische Lage eines Ortes auf der [[Erde]] anzugeben, können verschiedene [[:de:Koordinatensystem|Koordinatensystem]]e werden verwendet. Die geographischen Koordinaten sind aber die am häufigsten verwendete Möglichkeit, die Lage auf der Erdoberfläche zu beschreiben. | ||
| − | Die geographischen Koordinaten im eigentlichen Sinne sind [[geografische Länge]] (früher ''Längengrad''), [[geografische Breite]] (früher ''Breitengrad''). | + | Die geographischen Koordinaten im eigentlichen Sinne sind [[geografische Länge]] (früher ''Längengrad''), [[geografische Breite]] (früher ''Breitengrad''). Die Breitengrade werden dabei vom [[:de:Äquator|Äquator]] aus gezählt, die Pole liegen bei 90° Nord bzw. Süd, die Längengrade werden von einem willkürlichen [[Nullmeridian]] nach Osten und Westen gezählt bis 180°. Bis Anfang des 20. Jahrhunderts waren in verschiedenen Ländern verschiedene Nullmeridiane gebräuchlich, heutzutage wird der Meridian von [[:de:eenwich|Greenwich]] (Sternwarte in London) international verwendet. |
| − | Das | + | Das geographische Koordinatensystem ist mit der Angabe der geographischen Länge L und der geographischen Breite B gegeben. Diese beziehen sich auf den Nullmeridian und die Äquatorebene. Die geographische Länge eines Punktes P ist der Winkel zwischender Ebene durch den Nullmeridian und der Meridianebene im Punkt P. Die geographische Breite ist der Winkel, den die Flächennormale im Punkt P mit der Äquatorebene bildet. |
| − | + | == Ellipsoidische Koordinatensysteme == | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | == Ellipsoidische | + | |
[[Image:Ellipse mit großer und kleiner Halbachse.jpg|thumb|200px|Ellipse mit großer und kleiner Halbachse]] | [[Image:Ellipse mit großer und kleiner Halbachse.jpg|thumb|200px|Ellipse mit großer und kleiner Halbachse]] | ||
| − | Die Erdfigur kann in guter Näherung durch ein '''[[Ellipsoid]]''' beschrieben werden. | + | Die Erdfigur kann in guter Näherung durch ein '''[[Ellipsoid]]''' beschrieben werden. Dieses Ellipsoid entsteht durch die Rotation einer [[Meridian]]ellipse um die Erdrotationsachse oder eine Parallele hierzu. Eine solche Meridianellipse wird beschrieben durch die große Halbachse a und die kleine Halbachse b (siehe Abbildung). |
| − | Dieses Ellipsoid entsteht durch die Rotation einer [[Meridian]]ellipse um die Erdrotationsachse oder eine Parallele hierzu. Eine solche Meridianellipse wird beschrieben durch die große Halbachse a und die kleine Halbachse b (siehe Abbildung). | + | |
=== Lokal bestangepasste Ellipsoide === | === Lokal bestangepasste Ellipsoide === | ||
| − | Da Geodäten in früheren Jahrhunderten die vielen regionalen Abweichungen der Erdoberfläche vom Ellipsoid dadurch ausglichen, dass sie im betreffenden Gebiet ein bestangepasstes Ellipsoid berechneten, dessen Rotationsachse parallel, aber meist nicht identisch mit der Erdachse war, entstanden Dutzende geodätische Systeme als Bezugssysteme für Landesvermessungen und Kartenwerke. Mit der Entwicklung der [[Global Positioning System|Satellitennavigation]] musste ein weltweit einheitliches System geschaffen werden (siehe [[WGS84]]). | + | Da Geodäten in früheren Jahrhunderten die vielen regionalen Abweichungen der Erdoberfläche vom Ellipsoid dadurch ausglichen, dass sie im betreffenden Gebiet ein bestangepasstes Ellipsoid berechneten, dessen Rotationsachse parallel, aber meist nicht identisch mit der Erdachse war, entstanden Dutzende geodätische Systeme als Bezugssysteme für Landesvermessungen und Kartenwerke, die die ''Lagerung'' des jeweiligen Ellipsoids beschreiben. Mit der Entwicklung der [[Global Positioning System|Satellitennavigation]] musste ein weltweit einheitliches System geschaffen werden (siehe [[WGS84]]). |
| − | + | == Sphärische Koordinatensysteme == | |
| − | + | Zur Darstellung großer Teile der Erdoberfläche in kleinen Maßstäben eignet sich die Annäherung der Erdfigur durch eine Kugel. | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
== Ebene Koordinatensysteme == | == Ebene Koordinatensysteme == | ||
| Zeile 48: | Zeile 34: | ||
Rastersysteme (rechts)]] | Rastersysteme (rechts)]] | ||
| − | Auch für '''Rasterdaten''' läßt sich ein Koordinatensystem definieren. In diesem Koordinatensystem wird jedes einzelne Pixel durch seinen Zeilen- und Spaltenindex (m,n) als Koordinaten bezogen auf den Eckpunkt links oben als Nullpunkt mit dem Koordinaten (1,1), oftmals auch (0,0), eindeutig festgelegt. Somit erhält jedes Pixel ganzzahlige Koordinatenwerte. Wenn die Beziehung des Rasterbildes zur Erdoberfläche durch [[Georeferenzierung]] bestimmt wurde, können sie in "richtige" Koordinaten transformiert werden. | + | Auch für '''Rasterdaten''' läßt sich ein Koordinatensystem definieren. In diesem Koordinatensystem wird jedes einzelne Pixel durch seinen Zeilen- und Spaltenindex (m,n) als Koordinaten bezogen auf den Eckpunkt links oben als Nullpunkt mit dem Koordinaten (1,1), oftmals auch (0,0), eindeutig festgelegt. Somit erhält jedes Pixel ganzzahlige Koordinatenwerte. Wenn die Beziehung des Rasterbildes zur Erdoberfläche durch [[Georeferenzierung]] bestimmt wurde, können sie in "richtige" Koordinaten [[Koordinatentransformation|transformiert]] werden. |
| + | |||
| + | == Höhensysteme == | ||
| + | |||
| + | Die Höhenangaben werden aus praktischen Gründen nicht auf das Ellipsoid, sondern auf den unter den Kontinenten sich fortgesetzt gedachten Meeresspiegel, das [[Geoid]], bezogen. Dieses ist derart definiert, dass es die Lotlinie in jedem Punkt der Erde rechtwinklig schneidet. Da diese Definition schwereabhängig ist, muss bei Präzisionsnivellements auch die [[Erdschwere]] (Gravitation) bestimmt werden. | ||
| + | |||
| + | Bei der Festlegung des Meeresspiegels haben sich die verschiedenen Länder auf Pegel bezogen, die ihnen am nächsten lagen. | ||
| + | |||
| + | Normalnull (NN) bezeichnet den mittleren Wasserstand am Pegel von Amsterdam (für Deutschland), Österreich verwendet den Pegel von Triest und gibt Höhen über der Adria an, die Schweiz bezieht sich auf den Pegel von Marseille, und der Ostblock verwendete einheitlich den Kronstädter Pegel. | ||
| + | |||
| + | Moderne Messmethoden erfordern auch hier Änderungen. So werden Normalhöhen eingeführt und Höhenangaben (in Deutschland) nicht mehr auf NN, sondern auf NHN (Normalhöhennull) bezogen. | ||
== Dreidimensionale Koordinatensysteme == | == Dreidimensionale Koordinatensysteme == | ||
| Zeile 54: | Zeile 50: | ||
[[Image:Geozentrisches erdfestes XYZ - Koordinatensystem.jpg|thumb|250px|Geozentrisches erdfestes X,Y,Z - Koordinatensystem]] | [[Image:Geozentrisches erdfestes XYZ - Koordinatensystem.jpg|thumb|250px|Geozentrisches erdfestes X,Y,Z - Koordinatensystem]] | ||
| − | Im geozentrischen erdfesten X, Y, Z – Koordinatensystem wird ein Oberflächenpunkt P im [[:de:Erdschwerefeld|Erdschwerefeld]] bezogen auf eine mittlere Rotationsachse der Erde festgelegt (siehe Abbildung 1). Dabei bezeichnet S den Erdschwerpunkt (Geozentrum). Die Z-Achse fällt mit der mittleren Rotationsachse der Erde zusammen. Die X, Y – Ebene wird durch die Äquatorebene gebildet, während die X, Z – Ebene durch die mittlere [[Meridian]]ebene durch [[:de:Greenwich|Greenwich]] festgelegt wird. Anwendung findet dieses Koordinatensystem bei der Positionsbestimmung und Bahnbestimmung von[[:de:Satellit|Satellit]]en. | + | Im geozentrischen erdfesten X, Y, Z – Koordinatensystem wird ein Oberflächenpunkt P im [[:de:Erdschwerefeld|Erdschwerefeld]] bezogen auf eine mittlere Rotationsachse der Erde festgelegt (siehe Abbildung 1). Dabei bezeichnet S den Erdschwerpunkt (Geozentrum). Die Z-Achse fällt mit der mittleren Rotationsachse der Erde zusammen. Die X, Y – Ebene wird durch die Äquatorebene gebildet, während die X, Z – Ebene durch die mittlere [[Meridian]]ebene durch [[:de:Greenwich|Greenwich]] festgelegt wird. Anwendung findet dieses Koordinatensystem bei der Positionsbestimmung und Bahnbestimmung von [[:de:Satellit|Satellit]]en. |
== Nutzung von Koordinaten == | == Nutzung von Koordinaten == | ||
| Zeile 60: | Zeile 56: | ||
=== Karten === | === Karten === | ||
| − | In Land- oder Seekarten, die fast immer auf früheren Systemen beruhen, könnte eine Angabe in einem falschen Bezugssystem (etwa das Eintragen einer GPS-Position) einen Fehler von etlichen Hundert Metern verursachen, wenn das [[Geodätisches Datum|Kartendatum oder (Geodätische) Bezugssystem]] der Angabe nicht dasselbe ist wie das der Karte. Bei Angaben, die genauer als 1 km sein sollen, muss daher das Bezugssystem mit angegeben werden. Werte können dabei von einem System zu einem anderen umgerechnet werden (Koordinatentransformation). | + | In Land- oder Seekarten, die fast immer auf früheren Systemen beruhen, könnte eine Angabe in einem falschen Bezugssystem (etwa das Eintragen einer GPS-Position) einen Fehler von etlichen Hundert Metern verursachen, wenn das [[Geodätisches Datum|Kartendatum oder (Geodätische) Bezugssystem]] der Angabe nicht dasselbe ist wie das der Karte. Bei Angaben, die genauer als 1 km sein sollen, muss daher das Bezugssystem mit angegeben werden. Werte können dabei von einem System zu einem anderen umgerechnet werden ([[Koordinatentransformation]]). |
=== Luftfahrt und Nautik === | === Luftfahrt und Nautik === | ||
| Zeile 74: | Zeile 70: | ||
Im [[Vermessung]]swesen sind cm-Genauigkeiten gefragt - daher genügt die Angabe von [[Bogensekunden]] nicht, da eine Bogensekunde (1") etwa 31 m (Breitenangabe) bzw. 20 m (Längenangaben in Europa) entspricht. Meistens wird die Lage der [[Festpunkt]]e auf mm genau als [[Gauß-Krüger-Koordinate]] angegeben. | Im [[Vermessung]]swesen sind cm-Genauigkeiten gefragt - daher genügt die Angabe von [[Bogensekunden]] nicht, da eine Bogensekunde (1") etwa 31 m (Breitenangabe) bzw. 20 m (Längenangaben in Europa) entspricht. Meistens wird die Lage der [[Festpunkt]]e auf mm genau als [[Gauß-Krüger-Koordinate]] angegeben. | ||
| − | Bei der Detailvermessung, | + | Bei der Detailvermessung, insbesondere im [[Liegenschaftskataster]], wurden vor der generellen Einführung der Polarvermessung örtliche ebene Koordinatensysteme verwendet, die durch Messungslinien aufgespannt wurden und durch Einhängen in das Festpunktnetz die Berechnung von Landeskoordinaten ermöglichten. |
== Siehe auch == | == Siehe auch == | ||
| − | *[[ | + | *[[Koordinatentransformation]] |
*[[Polarkoordinate]] | *[[Polarkoordinate]] | ||
*[[Gauß-Krüger-Koordinatensystem]] | *[[Gauß-Krüger-Koordinatensystem]] | ||
Aktuelle Version vom 14. März 2007, 12:27 Uhr
Zur Festlegung eines Punktes auf der Erde werden Koordinatensysteme verwendet, die geeignet sind, den dreidimensionalen Raum abzubilden. Üblicherweise benutzt man rechtwinklige sphärische oder ebene Lagekoordinaten auf einer Bezugsfläche, die eine Annäherung der Erdoberfläche bildet, ergänzt um eine Höhenangabe, meist auf einer anderen Bezugsfläche, die angenähert die Meeresoberfläche ist. Die Raumfahrt, die EDV und insbesondere das Global Positioning System (GPS) haben dazu geführt, dass Koordinatenberechnungen nunmehr auch in rechtwinkligen X, Y, Z-Koordinatensystemen ausgeführt werden.
Die Lagebezugsflächen werden werden auch als Geodätisches Datum oder Geodätisches Bezugssystem bezeichnet. In moderne Bezugssyteme (WGS84 usw.) wird auch die Höhenbezugsfläche mit einbezogen.
Inhaltsverzeichnis
Geographische Koordinaten
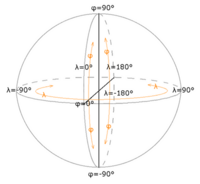
Um die geografische Lage eines Ortes auf der Erde anzugeben, können verschiedene Koordinatensysteme werden verwendet. Die geographischen Koordinaten sind aber die am häufigsten verwendete Möglichkeit, die Lage auf der Erdoberfläche zu beschreiben.
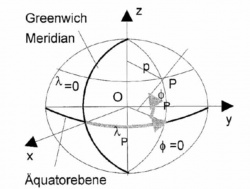
Die geographischen Koordinaten im eigentlichen Sinne sind geografische Länge (früher Längengrad), geografische Breite (früher Breitengrad). Die Breitengrade werden dabei vom Äquator aus gezählt, die Pole liegen bei 90° Nord bzw. Süd, die Längengrade werden von einem willkürlichen Nullmeridian nach Osten und Westen gezählt bis 180°. Bis Anfang des 20. Jahrhunderts waren in verschiedenen Ländern verschiedene Nullmeridiane gebräuchlich, heutzutage wird der Meridian von Greenwich (Sternwarte in London) international verwendet.
Das geographische Koordinatensystem ist mit der Angabe der geographischen Länge L und der geographischen Breite B gegeben. Diese beziehen sich auf den Nullmeridian und die Äquatorebene. Die geographische Länge eines Punktes P ist der Winkel zwischender Ebene durch den Nullmeridian und der Meridianebene im Punkt P. Die geographische Breite ist der Winkel, den die Flächennormale im Punkt P mit der Äquatorebene bildet.
Ellipsoidische Koordinatensysteme
Die Erdfigur kann in guter Näherung durch ein Ellipsoid beschrieben werden. Dieses Ellipsoid entsteht durch die Rotation einer Meridianellipse um die Erdrotationsachse oder eine Parallele hierzu. Eine solche Meridianellipse wird beschrieben durch die große Halbachse a und die kleine Halbachse b (siehe Abbildung).
Lokal bestangepasste Ellipsoide
Da Geodäten in früheren Jahrhunderten die vielen regionalen Abweichungen der Erdoberfläche vom Ellipsoid dadurch ausglichen, dass sie im betreffenden Gebiet ein bestangepasstes Ellipsoid berechneten, dessen Rotationsachse parallel, aber meist nicht identisch mit der Erdachse war, entstanden Dutzende geodätische Systeme als Bezugssysteme für Landesvermessungen und Kartenwerke, die die Lagerung des jeweiligen Ellipsoids beschreiben. Mit der Entwicklung der Satellitennavigation musste ein weltweit einheitliches System geschaffen werden (siehe WGS84).
Sphärische Koordinatensysteme
Zur Darstellung großer Teile der Erdoberfläche in kleinen Maßstäben eignet sich die Annäherung der Erdfigur durch eine Kugel.
Ebene Koordinatensysteme
Für praktische Arbeiten mit geringer räumlicher Ausdehnung wählt man oftmals ebene Koordinatensysteme. Ein ebenes geodätisches Koordinatensystem ist ein kartesisches x, y – Koordinatensystem, in dem die positive x-Achse (Ordinatenachse = Hochwert) nach Norden und die positive y-Achse (Abszissenachse = Rechtswert) nach Osten gerichtet ist. Die Lage eines Punktes in einem solchen Koordinatensystem ist durch die Angabe des Koordinatenpaares (x,y) eindeutig festgelegt. Das mathematische Koordinatensystem definiert dagegen x als die Abszissenachse und y als die Ordinate. Im bisher verwendeten geodätischen Koordinatensystem zeigt y den Rechtswert und x den Hochwert an.
Bezogen auf einen Punkt kann durch die Angabe einer Strecke s und eines Richtungswinkels t jeder andere Punkt in einem Polarkoordinatensystem angegeben werden. Diese beiden Koordinatensysteme können problemlos unter Nutzung trigonometrischer Beziehungen ineinander überführt werden.
Auch für Rasterdaten läßt sich ein Koordinatensystem definieren. In diesem Koordinatensystem wird jedes einzelne Pixel durch seinen Zeilen- und Spaltenindex (m,n) als Koordinaten bezogen auf den Eckpunkt links oben als Nullpunkt mit dem Koordinaten (1,1), oftmals auch (0,0), eindeutig festgelegt. Somit erhält jedes Pixel ganzzahlige Koordinatenwerte. Wenn die Beziehung des Rasterbildes zur Erdoberfläche durch Georeferenzierung bestimmt wurde, können sie in "richtige" Koordinaten transformiert werden.
Höhensysteme
Die Höhenangaben werden aus praktischen Gründen nicht auf das Ellipsoid, sondern auf den unter den Kontinenten sich fortgesetzt gedachten Meeresspiegel, das Geoid, bezogen. Dieses ist derart definiert, dass es die Lotlinie in jedem Punkt der Erde rechtwinklig schneidet. Da diese Definition schwereabhängig ist, muss bei Präzisionsnivellements auch die Erdschwere (Gravitation) bestimmt werden.
Bei der Festlegung des Meeresspiegels haben sich die verschiedenen Länder auf Pegel bezogen, die ihnen am nächsten lagen.
Normalnull (NN) bezeichnet den mittleren Wasserstand am Pegel von Amsterdam (für Deutschland), Österreich verwendet den Pegel von Triest und gibt Höhen über der Adria an, die Schweiz bezieht sich auf den Pegel von Marseille, und der Ostblock verwendete einheitlich den Kronstädter Pegel.
Moderne Messmethoden erfordern auch hier Änderungen. So werden Normalhöhen eingeführt und Höhenangaben (in Deutschland) nicht mehr auf NN, sondern auf NHN (Normalhöhennull) bezogen.
Dreidimensionale Koordinatensysteme
Im geozentrischen erdfesten X, Y, Z – Koordinatensystem wird ein Oberflächenpunkt P im Erdschwerefeld bezogen auf eine mittlere Rotationsachse der Erde festgelegt (siehe Abbildung 1). Dabei bezeichnet S den Erdschwerpunkt (Geozentrum). Die Z-Achse fällt mit der mittleren Rotationsachse der Erde zusammen. Die X, Y – Ebene wird durch die Äquatorebene gebildet, während die X, Z – Ebene durch die mittlere Meridianebene durch Greenwich festgelegt wird. Anwendung findet dieses Koordinatensystem bei der Positionsbestimmung und Bahnbestimmung von Satelliten.
Nutzung von Koordinaten
Karten
In Land- oder Seekarten, die fast immer auf früheren Systemen beruhen, könnte eine Angabe in einem falschen Bezugssystem (etwa das Eintragen einer GPS-Position) einen Fehler von etlichen Hundert Metern verursachen, wenn das Kartendatum oder (Geodätische) Bezugssystem der Angabe nicht dasselbe ist wie das der Karte. Bei Angaben, die genauer als 1 km sein sollen, muss daher das Bezugssystem mit angegeben werden. Werte können dabei von einem System zu einem anderen umgerechnet werden (Koordinatentransformation).
Luftfahrt und Nautik
Genauere Positionsangaben sind in der Luftfahrt und Nautik erforderlich. Hier wird die geografische Breite und Länge auf Bogenminuten genau angegeben, z. B. Zugspitze Lat = 47° 25' N, Lon = 10° 59' E oder Ost.
- Bogenminuten werden dezimal weiter unterteilt.
- Gemäß DIN 13.312, gültig für Luft- und Seefahrt, wird die geografische Breite mit Lat oder älter auch φ abgekürzt, die geografische Länge mit Lon oder λ. B und L bezeichnen geodätische Koordinaten und sind daher nicht normgemäß.
- Eine Breitenminute entspricht auf der Erdoberfläche einer Strecke von 1.852 m und definiert die Länge einer Seemeile.
- Die Strecke, die einer Längenminute entspricht, beträgt zwar am Äquator ebenfalls 1.852 m, nimmt aber zum Pol hin bis auf Null ab. Sie ist also breitenabhängig. Innerhalb Europas liegt die Strecke zwischen 1 km und 1,5 km.
Vermessungswesen
Im Vermessungswesen sind cm-Genauigkeiten gefragt - daher genügt die Angabe von Bogensekunden nicht, da eine Bogensekunde (1") etwa 31 m (Breitenangabe) bzw. 20 m (Längenangaben in Europa) entspricht. Meistens wird die Lage der Festpunkte auf mm genau als Gauß-Krüger-Koordinate angegeben.
Bei der Detailvermessung, insbesondere im Liegenschaftskataster, wurden vor der generellen Einführung der Polarvermessung örtliche ebene Koordinatensysteme verwendet, die durch Messungslinien aufgespannt wurden und durch Einhängen in das Festpunktnetz die Berechnung von Landeskoordinaten ermöglichten.
Siehe auch
- Koordinatentransformation
- Polarkoordinate
- Gauß-Krüger-Koordinatensystem
- UTM-Koordinatensystem
- Orthodrome
Weblinks
Allgemeine Informationen
- deutsche Wikipedia "Koordinatensystem"
- "geographic_coordinate_system" - Petrotechnical Open Standards Consortium
- "Basics": Von Graden, Minuten und Sekunden ...
- Umrechnung von Gradangaben (Altgrad / Neugrad) (Online)
- Geokoordinaten und administrative Informationen